Diffie-Hellman key exchange (exponential key exchange)
What is Diffie-Hellman key exchange (exponential key exchange)?
Diffie-Hellman key exchange is a method of digital encryption that securely exchanges cryptographic keys between two parties over a public channel without their conversation being transmitted over the internet. The two parties use symmetric cryptography to encrypt and decrypt their messages. Published in 1976 by Whitfield Diffie and Martin Hellman, it was one of the first practical examples of public key cryptography.
Diffie-Hellman key exchange raises numbers to a selected power to produce decryption keys. The components of the keys are never directly transmitted, making the task of a would-be code breaker mathematically overwhelming. The method doesn't share information during the key exchange. The two parties have no prior knowledge of each other, but the two parties create a key together.
Where is Diffie-Hellman key exchange used?
Diffie-Hellman key exchange's goal is to securely establish a channel to create and share a key for symmetric key algorithms. Generally, it's used for encryption, password-authenticated key agreement and forward security. Password-authenticated key agreements are used to prevent man-in-the-middle (MitM) attacks. Forward secrecy-based protocols protect against the compromising of keys by generating new key pairs for each session.
Diffie-Hellman key exchange is commonly found in security protocols, such as Transport Layer Security (TLS), Secure Shell (SSH) and IP Security (IPsec). For example, in IPsec, the encryption method is used for key generation and key rotation.
Even though Diffie-Hellman key exchange can be used for establishing both public and private keys, the Rivest-Shamir-Adleman algorithm, or RSA algorithm, can also be used, since it's able to sign public key certificates.
How does Diffie-Hellman key exchange work?
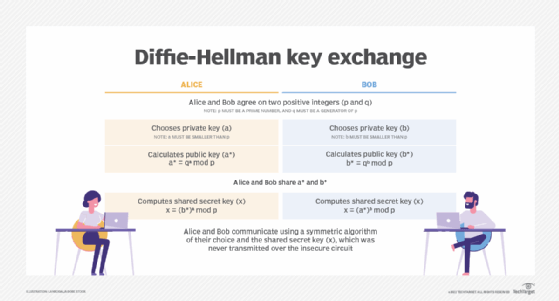
To implement Diffie-Hellman, two end users, Alice and Bob, mutually agree on positive whole numbers p and q, such that p is a prime number and q is a generator of p. The generator q is a number that, when raised to positive whole-number powers less than p, never produces the same result for any two such whole numbers. The value of p may be large, but the value of q is usually small.
Once Alice and Bob have agreed on p and q in private, they choose positive whole-number personal keys a and b. Both are less than the prime number modulus p. Neither user divulges their personal key to anyone; ideally, they memorize these numbers and don't write them down or store them anywhere. Next, Alice and Bob compute public keys a* and b* based on their personal keys according to the following formulas:
a* = qa mod p
b* = qb mod p
The two users can share their public keys a* and b* over a communications medium assumed to be insecure, such as the internet or a corporate wide area network. From these public keys, a number x can be generated by either user on the basis of their own personal keys. Alice computes x using the following formula:
x = (b*) mod p
Bob computes x using the following formula:
x = (a*) mod p
The value of x turns out to be the same according to either of the above two formulas. However, the personal keys a and b, which are critical in the calculation of x, haven't been transmitted over a public medium. Because it's a large and apparently random number, a potential hacker has almost no chance of correctly guessing x, even with the help of a powerful computer to conduct millions of trials. The two users can, therefore, in theory, communicate privately over a public medium with an encryption method of their choice using the decryption key x.
Vulnerabilities of Diffie-Hellman key exchange
The most serious limitation of Diffie-Hellman in its basic form is the lack of authentication. Communications using Diffie-Hellman by itself are vulnerable to MitM. Ideally, Diffie-Hellman should be used in conjunction with a recognized authentication method, such as digital signatures, to verify the identities of the users over the public communications medium.
Diffie-Hellman key exchange is also vulnerable to logjam attacks, specifically against the TLS protocol. Logjam attacks downgrade TLS connections to 512-bit cryptography, enabling an attacker to read and modify data that's passed through the connection. Diffie-Hellman key exchange can still be secure if implemented correctly. For example, logjam attacks won't work with a 2,048-bit key.
Examples of Diffie-Hellman key exchange
If two people, say Alice and Bob, want to communicate sensitive data over an open public network but want to avoid hackers or eavesdroppers, they can use Diffie-Hellman key exchange method for encryption. This open public network could be at a cafe, for example.
Alice and Bob privately choose a secret key, and a function is run on these keys to create a public key. The results -- and not the function -- are shared. Even if a third party is listening in, that third party won't have all the involved numbers, making it difficult to derive the function the numbers came from.
From here, Alice and Bob each run a new function using the results they received from the opposite party, their own secret number and the original prime value. Alice and Bob then arrive at a common shared secret key that a third party can't deduce. Alice and Bob are now free to communicate without worrying about third parties.
Learn more about cryptography basics, like symmetric key encryption.






