quantum cryptography
What is quantum cryptography?
Quantum cryptography is a method of encryption that uses the naturally occurring properties of quantum mechanics to secure and transmit data in a way that cannot be hacked.
Cryptography is the process of encrypting and protecting data so that only the person who has the right secret key can decrypt it. Quantum cryptography is different from traditional cryptographic systems in that it relies on physics, rather than mathematics, as the key aspect of its security model.
Quantum cryptography is a system that is completely secure against being compromised without the knowledge of the message sender or the receiver. That is, it is impossible to copy or view data encoded in a quantum state without alerting the sender or receiver. Quantum cryptography should also remain safe against those using quantum computing as well.
Quantum cryptography uses individual particles of light, or photons, to transmit data over fiber optic wire. The photons represent binary bits. The security of the system relies on quantum mechanics. These secure properties include the following:
- particles can exist in more than one place or state at a time;
- a quantum property cannot be observed without changing or disturbing it; and
- whole particles cannot be copied.
These properties make it impossible to measure the quantum state of any system without disturbing that system.
Photons are used for quantum cryptography because they offer all the necessary qualities needed: Their behavior is well understood, and they are information carriers in optical fiber cables. One of the best-known examples of quantum cryptography currently is quantum key distribution (QKD), which provides a secure method for key exchange.
How does quantum cryptography work?
In theory, quantum cryptography works by following a model that was developed in 1984.
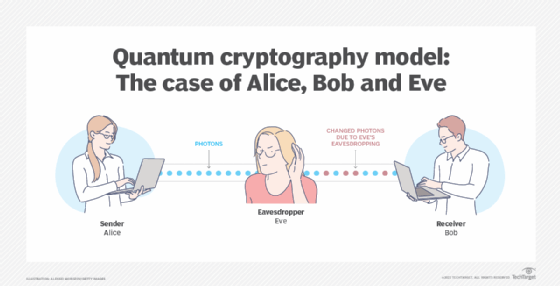
The model assumes there are two people named Alice and Bob who wish to exchange a message securely. Alice initiates the message by sending Bob a key. The key is a stream of photons that travel in one direction. Each photon represents a single bit of data -- either a 0 or 1. However, in addition to their linear travel, these photons are oscillating, or vibrating, in a certain manner.
So, before Alice, the sender, initiates the message, the photons travel through a polarizer. The polarizer is a filter that enables certain photons to pass through it with the same vibrations and lets others pass through in a changed state of vibration. The polarized states could be vertical (1 bit), horizontal (0 bit), 45 degrees right (1 bit) or 45 degrees left (0 bit). The transmission has one of two polarizations representing a single bit, either 0 or 1, in either scheme she uses.
The photons now travel across optical fiber from the polarizer toward the receiver, Bob. This process uses a beam splitter that reads the polarization of each photon. When receiving the photon key, Bob does not know the correct polarization of the photons, so one polarization is chosen at random. Alice now compares what Bob used to polarize the key and then lets Bob know which polarizer she used to send each photon. Bob then confirms if he used the correct polarizer. The photons read with the wrong splitter are then discarded, and the remaining sequence is considered the key.
Let's suppose there is an eavesdropper present, named Eve. Eve attempts to listen in and has the same tools as Bob. But Bob has the advantage of speaking to Alice to confirm which polarizer type was used for each photon; Eve doesn't. Eve ends up rendering the final key incorrectly.
Alice and Bob would also know if Eve was eavesdropping on them. Eve observing the flow of photons would then change the photon positions that Alice and Bob expect to see.
What quantum cryptography is used for and examples
Quantum cryptography enables users to communicate more securely compared to traditional cryptography. After keys are exchanged between the involved parties, there is little concern that a malicious actor could decode the data without the key. If the key is observed when it is being constructed, the expected outcome changes, alerting both the sender and the receiver.
This method of cryptography has yet to be fully developed; however, there have been successful implementations of it:
- The University of Cambridge and Toshiba Corp. created a high-bit rate QKD system using the BB84 quantum cryptography protocol.
- The Defense Advanced Research Projects Agency Quantum Network, which ran from 2002 to 2007, was a 10-node QKD network developed by Boston University, Harvard University and IBM Research.
- Quantum Xchange launched the first quantum network in the U.S., featuring 1,000 kilometers (km) of fiber optic cable.
- Commercial companies, such as ID Quantique, Toshiba, Quintessence Labs and MagiQ Technologies Inc., also developed commercial QKD systems.
In addition to QKD, some of the more notable protocols and quantum algorithms used in quantum cryptography are the following:
- quantum coin flipping;
- position-based quantum cryptography; and
- device-independent quantum cryptography.
Benefits of quantum cryptography
Benefits that come with quantum cryptography include the following:
- Provides secure communication. Instead of difficult-to-crack numbers, quantum cryptography is based on the laws of physics, which is a more sophisticated and secure method of encryption.
- Detects eavesdropping. If a third party attempts to read the encoded data, then the quantum state changes, modifying the expected outcome for the users.
- Offers multiple methods for security. There are numerous quantum cryptography protocols used. Some, like QKD, for example, can combine with classical encryption methods to increase security.
Limitations of quantum cryptography
Potential downsides and limitations that come with quantum cryptography include the following:
- Changes in polarization and error rates. Photons may change polarization in transit, which potentially increases error rates.
- Range. The maximum range of quantum cryptography has typically been around 400 to 500 km, with the exception of Terra Quantum, as noted below.
- Expense. Quantum cryptography typically requires its own infrastructure, using fiber optic lines and repeaters.
- Number of destinations. It is not possible to send keys to two or more locations in a quantum channel.
Differences between traditional cryptography and quantum cryptography
The classic form of cryptography is the process of mathematically scrambling data, where only one person who has access to the right key can read it. Traditional cryptography has two different types of key distribution: symmetric key and asymmetric key. Symmetric key algorithms work by using a single key to encrypt and decrypt information, whereas asymmetric cryptography uses two keys -- a public key to encrypt messages and a private key to decode them. Traditional cryptography methods have been trusted since it would take an impractical time frame for classical computers to factor the needed large numbers that make up public and private keys.

Unlike traditional cryptography, which is based on mathematics, quantum cryptography is based on the laws of quantum mechanics. And, whereas traditional cryptography is based on mathematical computation, quantum cryptography is much harder to decrypt since the act of observing the involved photons changes the expected outcome, making both the sender and receiver aware of the presence of an eavesdropper. Quantum cryptography also typically has a distance or range associated with it since the process requires fiber optic cables and repeaters spaced out to boost the signal.
Future of quantum cryptography implementation
Quantum computers are in the early phases and need more development before a broad audience can start using quantum communications. Even though there are limitations to quantum cryptography, such as not being able to send keys to two locations at once, the field is still steadily growing.
Recent advances, for example, include improvements in range. Swiss quantum technology company Terra Quantum announced a breakthrough for quantum cryptography in terms of range. Previously, the distance for quantum cryptography was limited to a maximum of 400 to 500 km. Terra Quantum's development enables quantum cryptography keys to be transmitted over a distance of more than 40,000 km. Instead of building a new optical line filled with numerous repeaters, Terra Quantum's development enables quantum keys to be distributed inside standard optical fiber lines that are already being used in telecom networks.
Learn more about QKD, such as its potential ease of access and included risks.







