Secure Electronic Transaction (SET)
What is Secure Electronic Transaction (SET)?
Secure Electronic Transaction (SET) is a system and electronic protocol to ensure the integrity and security of transactions conducted over the internet. E-commerce websites implemented this early protocol to secure electronic payments made via debit and credit cards.
SET blocks out all personal details on the card, preventing hackers and data thieves from accessing or stealing the cardholder's information. The merchant also cannot see these personal details, which are transferred directly to the credit card company for user authentication and verification.
SET is not a payment system or gateway, but a set of security protocols. It uses some aspects of a Public Key Infrastructure (PKI) to address concerns around privacy, authenticity and security in e-commerce applications.
The primary goal of SET is to protect credit/debit card transactions as they take place online. It provides a secure and confidential transaction environment for everyone involved in the e-commerce transaction, including the customer and merchant. It also authenticates users with the help of digital certificates.

The development of SET can be traced to the emergence of e-commerce in the mid-1990s. SET was jointly designed by card companies Visa and Mastercard, with the aim of securing web browsers for card transactions. In its early days of development, SET was also supported by other organizations, including:
- technology firms like Microsoft and IBM;
- network infrastructure and internet services companies like Verisign; and
- web services company Netscape.
Microsoft provided the Secure Transaction Technology (STT) for SET, while Netscape provided the Secure Sockets Layer (SSL) technology.
Secure Electronic Transaction and cryptography
SET was designed to fulfill the requirements for e-commerce security that were not being fulfilled by SSL and Transport Layer Security (TLS). To secure card transactions and protect purchasing information, SET uses both symmetric (Data Encryption Standard or DES) and asymmetric (PKI) cryptography.
For key management, it uses PKI to reliably distribute public keys between participants.
SET uses 56-bit session keys which are transmitted asymmetrically. The remainder of the card transaction uses symmetric DES encryption. SET uses long keys for both kinds of encryption.
Secure Electronic Transaction and digital signatures
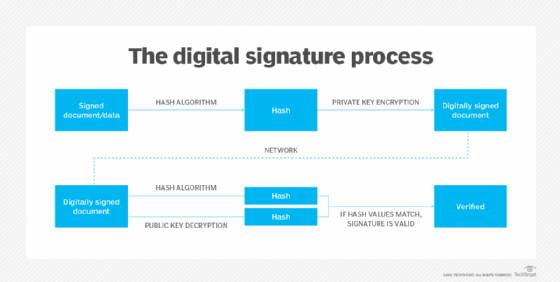
In SET, authentication and nonrepudiation are achieved through digital signatures so the parties in the transaction cannot deny that the transaction occurred. Every time a customer initiates an electronic purchase, an encrypted digital certificate is generated for the transaction's participants. This includes the customer, merchant and financial institution.
Matching digital keys are also generated, so participants can confirm the certificates of the other party and verify the transaction.
Using a hashing algorithm, SET signs electronic transactions using the sender's private key. This produces a series of values (message digest) that "sign" a message. The transaction's authenticity can be verified by comparing the transaction message and message digest with the sender's public key.
The algorithms used in SET ensure that only the party with the corresponding digital key can confirm the transaction, no one else.
Security architecture of Secure Electronic Transaction
The SET architecture (designed to support PKI) comprises:
Digital certificates
Digital signatures authenticate the merchant's and customer's identities to mitigate the risk of a malicious third party manipulating transaction information. The Certificate Authority (CA) issues digital certificates to the issuing bank. The card issuer and acquirer, which may be a bank or other financial institution, both play an important role in issuing digital certificates.
Dual signatures
In the SET scheme, the customer's order information and payment information are encrypted with separate public keys. The order information is encrypted with the merchant's public keys, and the payment information is encrypted with the acquiring bank's public keys.
This system ensures that the encrypted PI can only be decrypted by the acquiring bank, and the encrypted OI can only be decrypted by the merchant.
Digital wallet
SET enforces customer self-authentication by entering a password that activates their digital wallet. This happens before they initiate a payment transaction. Following the authentication, the customer's device (PC, phone, etc.) sends their order and payment information to the merchant. When the cardholder is authenticated, the issuing bank provides payment authorization to the acquiring bank, which then informs the merchant.
Secure Electronic Transaction participants
A number of participants are involved in the SET process:
- Cardholder/customer: The authorized holder of the payment card (Visa or Mastercard)
- E-commerce merchant: The seller
- Card issuer: A financial organization (e.g., bank) that issues the payment card
- Acquirer: A financial organization that processes payment authorization and facilitates electronic funds transfer to the merchant's account
- Payment gateway: Interface between card payment networks and secure electronic transactions
- Certificate Authority: Trusted organization that provides public key digital certificates
The drawbacks of Secure Electronic Transaction
When SET was first introduced in 1996 by the SET consortium (Visa, Mastercard, Microsoft, Verisign, etc.), it was expected to be widely adopted within the next few years. Industry experts also predicted that it would quickly become the key enabler of global ecommerce. However, this didn't quite happen due to some serious shortcomings in the protocol.
The security properties of SET are superior to SSL and the newer TLS, particularly in their ability to prevent e-commerce fraud. However, the biggest drawback of SET is its complexity. SET requires both customers and merchants to install special software -- card readers and digital wallets -- meaning that transaction participants had to complete more tasks to implement SET. This complexity also slowed down the speed of e-commerce transactions. SSL and TLS do not have such problems.
The overhead involved in PKI and the initialization and registration processes also stalled the widespread adoption of SET. Interoperability among SET products -- e.g., certificate translations and interpretations among trusted third parties with different certificate policies -- was also a significant problem with SET, which also was challenged by poor usability and the vulnerability of PKI.
The decline of Secure Electronic Transaction
Despite enthusiastic support for SET in the early days, support for the protocol has waned over time. Other security standards have emerged for online debit and credit card transactions for e-commerce.
Visa and other card providers including Mastercard and American Express eventually adopted the 3-D Secure framework for securing customers' digital payments. This XML-based protocol is designed to provide additional security for online credit/debit card transactions.








