
kras99 - stock.adobe.com
What is Triple DES and why is it being disallowed?
Triple DES no longer provides the encryption strength it once did. Prepare now to transition away from its use to a more security alternative.
Triple Data Encryption Algorithm is used widely across many industries and in many popular network protocols to encrypt data at rest and data in motion. NIST deprecated the algorithm in 2018, however, and Triple DES use will be disallowed after 2023.
What is Triple DES?
The Data Encryption Standard algorithm on which Triple DES is based was first published in 1975. DES is a symmetric key block cipher. Symmetric key block ciphers process fixed-size blocks simultaneously using the same key to encrypt the data. The block size of a cipher refers to the number of bits that are processed together.
The original DES algorithm specified the use of 56-bit keys. As computing advanced, this proved ineffective protection against certain attacks. The algorithm was retired in 2005.
In 1998, Triple Data Encryption Algorithm, commonly referred to as Triple DES, TDEA and, informally, 3DES, was introduced. It applies the DES cipher algorithm three times to each data block for more effective key length.
A brief history of DES and Triple DES
In the early 1970s, the National Bureau of Standards -- now NIST -- identified a need for a government-wide standard for encrypting unclassified, sensitive information. Early proposals for the new DES were not deemed acceptable. Then, a block cipher called Lucifer was submitted by IBM Corporation in 1974. After consultation with the National Security Agency (NSA), a modified version was approved as a Federal Information Processing Standard in 1976 and published on Jan. 15, 1977, as FIPS PUB 46. It was authorized for use on all unclassified data.
The most notable changes between the approved algorithm and the original Lucifer cipher were a reduced key size -- from 128 bits to 56 bits -- and substitution boxes (S-boxes) designed under classified conditions. An S-box is the component of the algorithm that performs substitution.
Many experts felt the smaller key size made DES more vulnerable to brute-force attacks and that the NSA had somehow introduced a backdoor into the algorithm to allow the agency to decrypt data encrypted by DES without needing to know the encryption key. It was discovered 13 years later that the S-boxes were secure against an attack known as differential cryptanalysis, which was only publicly discovered in 1990. This suggests the NSA was already aware of this attack in 1977.
Despite these criticisms, DES was quickly adopted and sparked a dramatic rise in the study and development of encryption algorithms. It was reaffirmed as the standard in 1983, 1988 and 1993.
Due to the ever-increasing processing power of computers, however, DES became vulnerable to brute-force attacks. Although a 56-bit key space amounts to approximately 72 quadrillion possibilities, this no longer provides required levels of security. The algorithm was retired in 2005.
To avoid the need to design a completely new cipher and to make replacing DES relatively straightforward, the Triple DES specification, FIPS PUB 46-3, was published in 1999. Now, it is reaching the same fate as its predecessor.
The Triple DES encryption process
Triple DES operates in three steps: Encrypt-Decrypt-Encrypt (EDE). It works by taking three 56-bit keys (K1, K2 and K3) known as a key bundle and encrypting first with K1, decrypting next with K2 and encrypting a last time with K3. A Triple DES two-key version exists, where the same algorithm runs three times but K1 is used for the first and last steps. This two-key variant was retired in 2015.
The algorithm is run three times because double enciphering can't be used. A class of attacks called meet-in-the-middle attacks encrypt from one end, decrypt from the other and look for collisions -- keys that produce the same answer in either direction. With sufficient memory, Double DES -- or any other cipher run twice -- would only be twice as strong as the base cipher. In other words, the double cipher would only be as strong as the same cipher run once but with a key that was one bit longer.
But that's not all: If the cipher forms a group, then encrypting twice with two keys is equivalent to encrypting once with some other key. It's not trivial to know what that other key is, but it does mean that a brute-force attack would find that third key as it tried all the possible single keys. So, if the cipher is a group, then multiple ciphering is a waste of time.
A group is a relationship between a set and an operator. If they behave more or less the way integers do with addition, they form a group. If you keep encrypting a block and it makes a full circuit over the set of possible blocks, that also forms a group.
DES is not a group. DES does, however, have known structural features in it that make people say it's not strongly not a group -- in other words, it might be a group. For example, known loops exist in DES where, if you keep encrypting with the same key, you run around in a long loop.
Triple DES encryption modes
With Triple DES, each of the three rounds can be run in either direction -- encrypt or decrypt -- using the DES algorithm. This results in eight different possible modes for Triple DES.
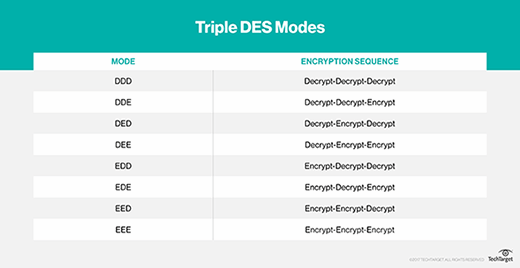
Those structural features are why you wouldn't want to use EEE or DDD mode if there were a better option, just as you wouldn't want to use EED, DEE, DDE or EDD. Because of the weak nongroupness of DES, EDE or DED compositions work best. Plus, EDE makes more sense. If you use DED, you have to explain why Triple DES starts with decryption.
The strength of Triple DES: Why it's being disallowed
The security strength of a cryptographic algorithm or system is specified in bits and is the expected amount of work -- that is, the base 2 logarithm of the number operations -- to cryptanalyze and break it.
If 2N execution operations of the algorithm are required to break a cryptographic algorithm and reveal the original plaintext, the algorithm's security strength is N bits. NIST policy assigns specific strength values from the set -- for example, 80, 112, 128, 192 and 256 -- and for symmetric ciphers. The value is typically equal to the key size of the cipher, which is equivalent to the complexity of a brute-force attack. A cryptographic algorithm is considered broken when an attack is found to have less than its advertised level of security, though not all attacks are necessarily practical.
When Triple DES is used with three independent keys, sometimes referred to as 3TDEA, it has a key length of 168 bits (3 x 56-bit DES keys = 168 independent key bits). Due to meet-in-the-middle attacks, however, the effective security 3TDEA provides is only 112 bits. Also, the small block size of 64 bits makes it vulnerable to block collision attacks when it's used to encrypt large amounts of data with the same key, such as an HTTPS session.
In 2016, researchers successfully exploited Triple DES' short block size (CVE-2016-2183) in various real-world protocols via a birthday attack called Sweet32. As a result, NIST restricted Triple DES use in 2017 to 8 MB of data using a single key bundle. This meant it could no longer effectively be used for TLS, IPsec or large file encryption.
In 2018, NIST published guidance that, after a period of public consultation, Triple DES would be deprecated for all new applications -- meaning, it could be used, but risk must be accepted -- and usage disallowed -- meaning no longer allowed for the indicated use -- after 2023.
What has replaced Triple DES?
NIST began a search for DES replacement algorithms in 1997. In 2000, Advanced Encryption Standard (AES) was chosen from 15 entries from around the world in an open competition. AES is more mathematically efficient and significantly faster than Triple DES, so it is ideal for applications, firmware and hardware that require low latency or high throughput.
AES is the first publicly accessible and open cipher approved by the NSA for top-secret information. It quickly became the de facto world encryption standard.
AES comprises three block ciphers -- AES-128, AES-192 and AES-256 -- with both software and hardware implementations being considered efficient. Each cipher has a 128-bit block size, with key sizes of 128, 192 and 256 bits, respectively, making it exponentially stronger than the 56-bit key of DES. There are 10 rounds for 128-bit keys, 12 rounds for 192-bit keys and 14 rounds for 256-bit keys. A round consists of several processing steps that convert the input plaintext into the final output of ciphertext.
Security experts consider AES safe against brute-force attacks, and all key lengths are deemed sufficient to protect classified information up to the secret level with top-secret information requiring either 192 or 256 key lengths.
Published as a FIPS 197 standard in 2001, AES was originally meant to be an alternative to Triple DES until 2030 to give everyone plenty of time to transition to AES.
Although five years -- 2018 to 2023 -- may seem ample time to make the switch from Triple DES to AES, updating legacy software and hardware could prove challenging, if not impossible, in some cases. For example, older hardware may not have the capability to process AES calculations. Certainly, during the transition period, organizations should change Triple DES keys more frequently. Even the most extensive cryptographic systems can be vulnerable if a hacker gains access to the encryption key.
Editor's note: This article includes previous coverage by Jon Callas.








