cryptology
What is cryptology?
Cryptology is the mathematics, such as number theory and the application of formulas and algorithms, that underpin cryptography and cryptanalysis. Cryptanalysis concepts are highly specialized and complex, so this discussion will concentrate on some of the key mathematical concepts behind cryptography, as well as modern examples of its use.
In order for data to be secured for storage or transmission, it must be transformed in such a manner that it would be difficult for an unauthorized individual to be able to discover its true meaning. To do this, security systems and software use certain mathematical equations that are very difficult to solve unless strict criteria are met. The level of difficulty of solving a given equation is known as its intractability. These equations form the basis of cryptography.
Types of cryptology equations
Some of the most important equations used in cryptology include the following.
The discrete logarithm problem
The best way to describe this problem is first to show how its inverse concept works. Assume we have a prime number, P (a number that is not divisible except by 1 and itself). This P is a large prime number of over 300 digits. Let us now assume we have two other integers, a and b. Now, say we want to find the value of N, so that value is found by the following formula:
N = ab mod P, where 0 ≤ N ≤ (P · 1)
This is known as discrete exponentiation and is quite simple to compute. However, the opposite is true when we invert it. If we are given P, a, and N and are required to find b so that the equation is valid, then we face a tremendous level of difficulty. This problem forms the basis for a number of public key infrastructure (PKI) algorithms, such as Diffie-Hellman and EIGamal.
The integer factorization problem
This is simple in concept. Say, someone takes two prime numbers, P2 and P1, which are both "large" (a relative term, the definition of which continues to move forward as computing power increases). We then multiply these two primes to produce the product, N. The difficulty arises when, being given N, we try to find the original P1 and P2. The Rivest-Shamir-Adleman PKI encryption protocol is one of many based on this problem. To simplify matters to a great degree, the N product is the public key, and the P1 and P2 numbers are, together, the private key.
The elliptic curve discrete logarithm problem
This is a cryptographic protocol based upon a reasonably well-known mathematical problem. Mathematicians have studied the properties of elliptic curves for centuries but only began applying them to the field of cryptography with the development of widespread computerized encryption in the 1970s.
First, imagine a huge piece of paper, on which is printed a series of vertical and horizontal lines. Each line represents an integer, with the vertical lines forming x class components and horizontal lines forming the y class components. The intersection of a horizontal and vertical line gives a set of coordinates (x,y). In the highly simplified example below, we have an elliptic curve that is defined by the equation:
y2 + y = x3 · x2
For the above, given a definable operator, we can determine any third point on the curve given any two other points. This definable operator forms a "group" of finite length. To add two points on an elliptic curve, we first need to understand that any straight line that passes through this curve intersects it at precisely three points. If we define two of these points as u and v, we can then draw a straight line through these points to find another intersecting point at w. We can then draw a vertical line through w to find the final intersecting point at x. Now, we can see that u + v = x. This rule works when we define another imaginary point, the origin, or O, which exists at theoretically extreme points on the curve. The problem appears to be quite intractable, requiring a shorter key length (thus, allowing for quicker processing time) for equivalent security levels as compared to the integer factorization problem and the discrete logarithm problem.
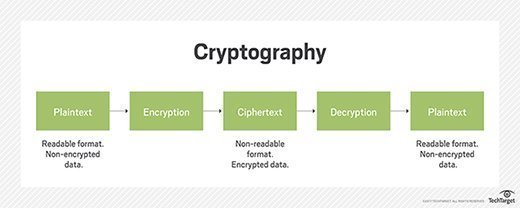
Modern cryptology examples
Today, researchers use cryptology as the basis for encryption in cybersecurity products and systems that protect data and communications. A few examples of modern applications include the following.
Symmetric-key cryptography. Symmetric-key cryptography, sometimes referred to as secret-key cryptography, uses the same key to encrypt and decrypt data. Encryption and decryption are inverse operations, meaning the same key can be used for both steps. Symmetric-key cryptography's most common form is a shared secret system, in which two parties have a shared piece of information, such as a password or passphrase, that they use as a key to encrypt and decrypt information to send to each other.
Public-key cryptography. Public-key cryptography is a cryptographic application that involves two separate keys -- one private and one public. While both keys are mathematically related to one another, only the public key can be used to decrypt what has been encrypted with the private key. The most well-known application of public-key cryptography is for digital signatures, which allow users to prove the authenticity of digital messages and documents. It also makes it possible to establish secure communications over insecure channels.
Cryptanalysis. Cryptanalysis is the practice of analyzing cryptographic systems in order to find flaws and vulnerabilities. For example, cryptanalysts attempt to decrypt ciphertexts without knowledge of the encryption key or algorithm used for encryption. Cryptanalysts use their research results to help to improve and strengthen or replace flawed algorithms.
Cryptographic primitives. A cryptographic primitive in cryptography is a basic cryptographic technique, such as a cipher or hash function, used to construct subsequent cryptographic protocols. In a common scenario, a cryptographic protocol begins by using some basic cryptographic primitives to construct a cryptographic system that is more efficient and secure.
Cryptosystems. Cryptosystems are systems used to encode and decode sensitive information. Cryptosystems incorporate algorithms for key generation, encryption and decryption techniques to keep data secure. The basic principle of a cryptosystem is the use of a ciphertext to transform data held in plaintext into an encrypted message.





